Count Sort

counting sort is a kind of sorting algorithm that sacrifices memory space for low time complexity, and it is also a kind of algorithm that is not based on comparison. The non-comparison-based sorting algorithm here means that there is no comparison size between array elements. We know that the divide-and-conquer method to solve the sorting problem can only make the time complexity of the algorithm approach Θ(nlogn) at the fastest, that is, the time complexity based on comparison has a lower bound Ω(nlog⁡n), and the sorting algorithm based on no comparison can break through this lower bound.

Algorithm description

• Find the largest and smallest elements of the array to be sorted;
• Count the number of occurrences of each element with value i in the array, stored in the i - th item of the array C;
• Add up all counts (starting with the first element in C and adding each term to the previous one);
• Backfill the target array: Place each element i in the C(i) item of the new array, and subtract 1 from C(i) for each element.

GIF presentation

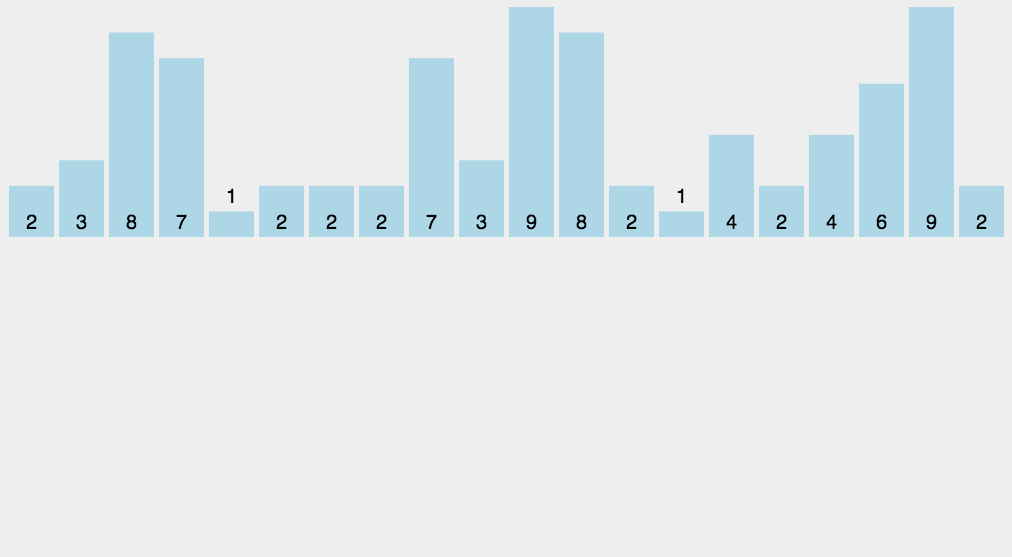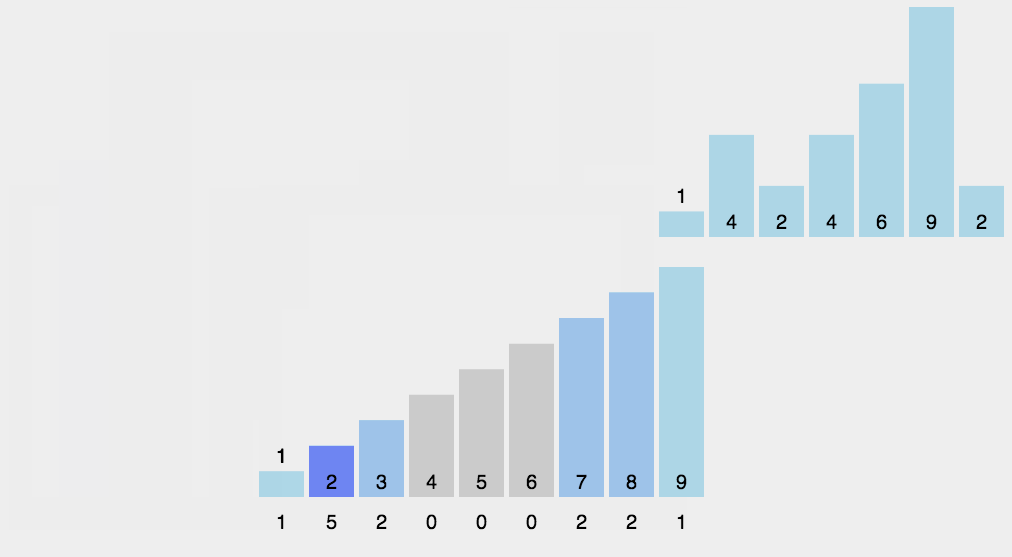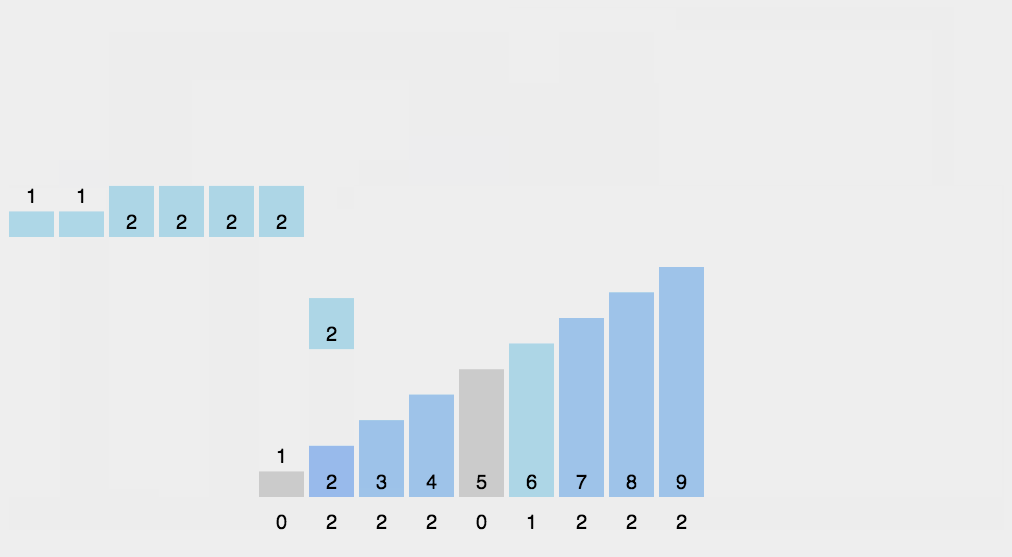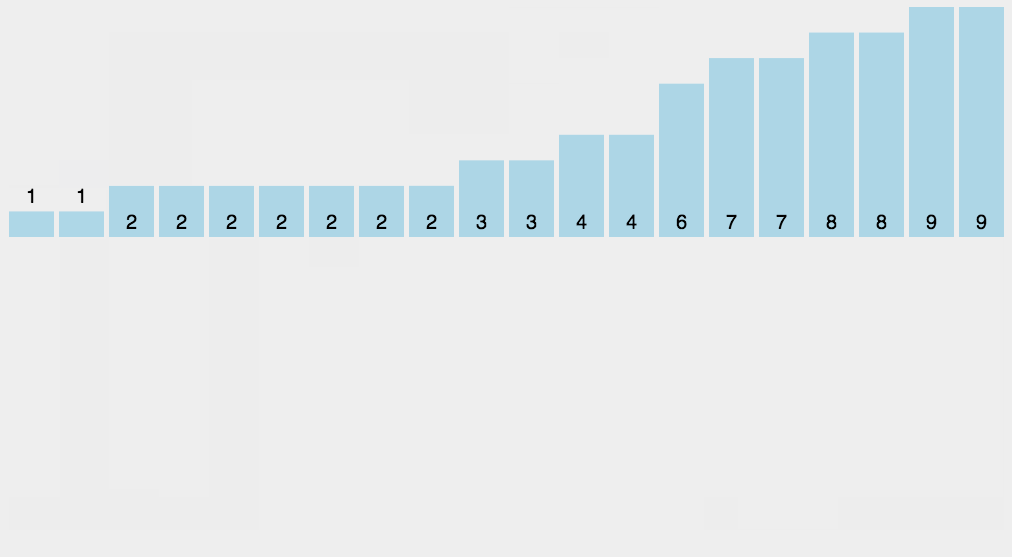
Code demo

const getMax = (list: number[]) => {
  let max = list[0];
  for (let i = 1; i < list.length; i++) {
    if (max < list[i]) {
      max = list[i];
    }
  }
  return max;
};
/**
 * @description: Count Sort
 * @param {Array<number>} list
 * @return {Array<number>}
 */
const count = (list: number[]): number[] => {
  if (list.length <= 1) return list;
  const max = getMax(list);
  const countList = new Array(max + 1).fill(0);
  list.forEach((item) => {
    if (!countList[item]) {
      countList[item] = 1;
    } else {
      countList[item]++;
    }
  });
  const result = [];
  for (let i = 0; i < countList.length; i++) {
    while (countList[i]) {
      result.push(i);
      countList[i]--;
    }
  }
  return result;
};

Algorithm analysis

Counting sort is a stable sorting algorithm. When the input elements are n integers between 0 and k, the time complexity is O(n+k) and the space complexity is also O(n+k), which sorts faster than any comparison sorting algorithm. Counting sort is an efficient sorting algorithm when k is not large and the sequence is concentrated.