计数排序（ Count Sort ）

计数排序（counting sort）就是一种牺牲内存空间来换取低时间复杂度的排序算法，同时它也是一种不基于比较的算法。这里的不基于比较指的是数组元素之间不存在比较大小的排序算法，我们知道，用分治法来解决排序问题最快也只能使算法的时间复杂度接近 Θ(nlogn)，即基于比较的时间复杂度存在下界 Ω(nlog⁡n)，而不基于比较的排序算法可以突破这一下界。

算法描述

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项；
• 对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素 i 放在新数组的第 C(i)项，每放一个元素就将 C(i)减去 1。

动图演示

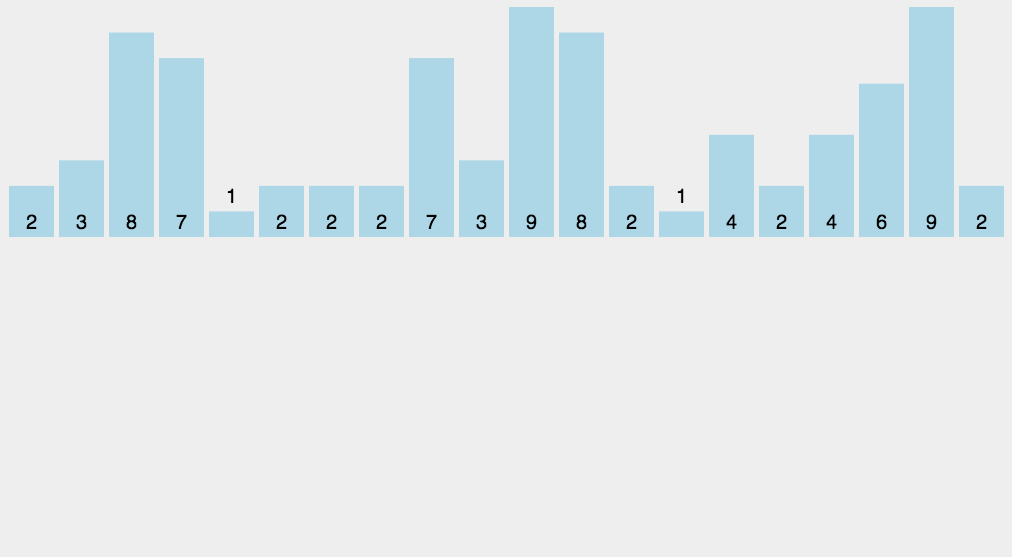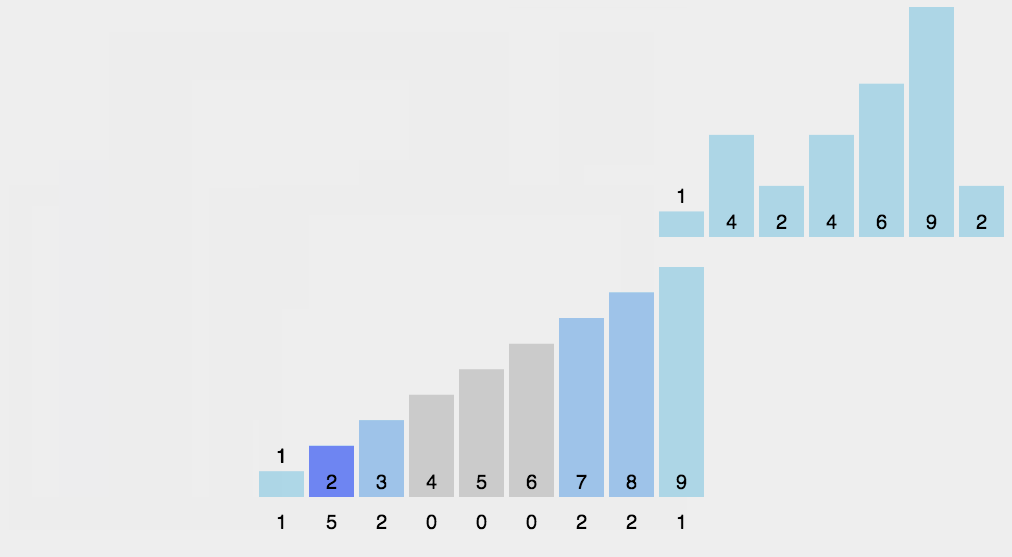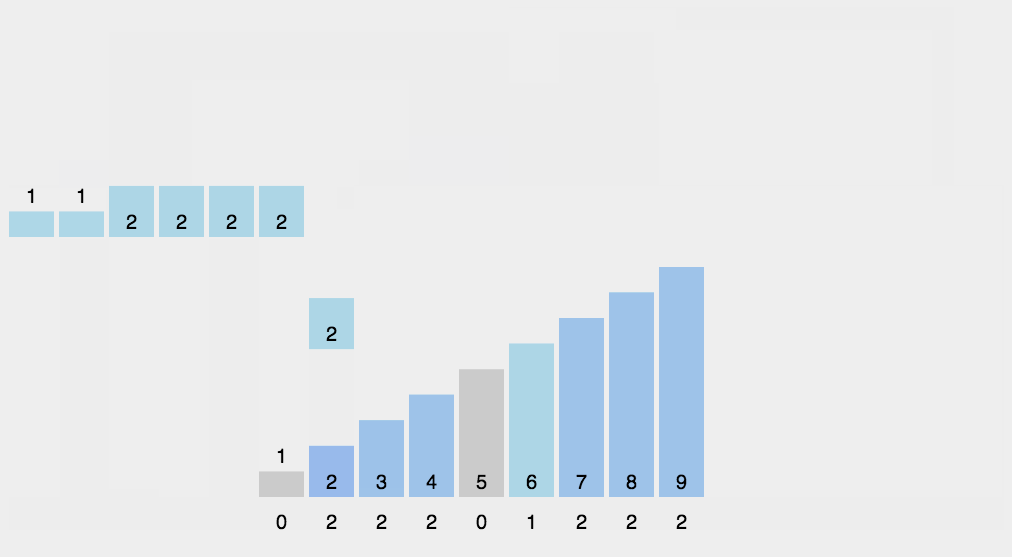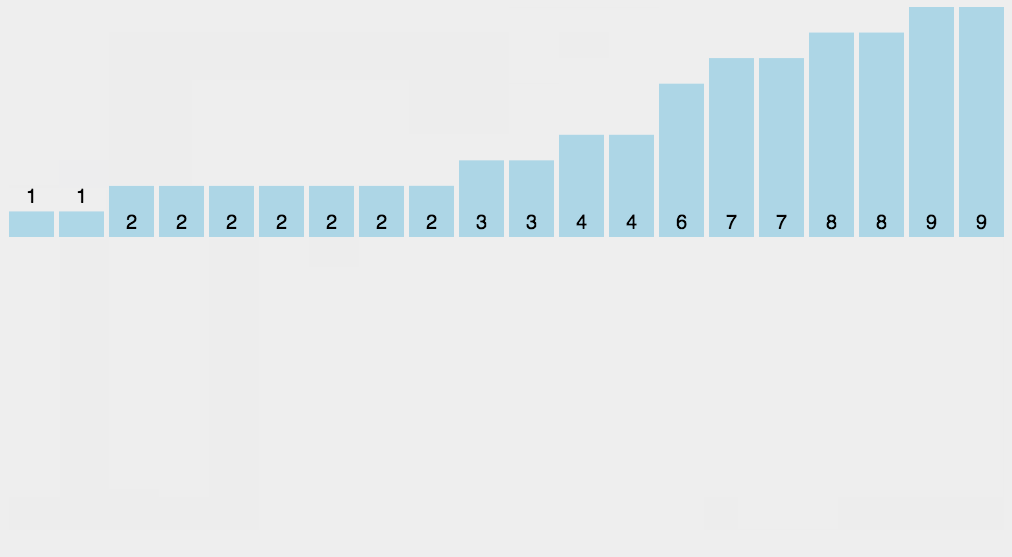
代码演示

const getMax = (list: number[]) => {
  let max = list[0];
  for (let i = 1; i < list.length; i++) {
    if (max < list[i]) {
      max = list[i];
    }
  }
  return max;
};
/**
 * @description: 计数排序
 * @param {Array<number>} list
 * @return {Array<number>}
 */
const count = (list: number[]): number[] => {
  if (list.length <= 1) return list;
  const max = getMax(list);
  const countList = new Array(max + 1).fill(0);
  list.forEach((item) => {
    if (!countList[item]) {
      countList[item] = 1;
    } else {
      countList[item]++;
    }
  });
  const result = [];
  for (let i = 0; i < countList.length; i++) {
    while (countList[i]) {
      result.push(i);
      countList[i]--;
    }
  }
  return result;
};

算法分析

计数排序是一个稳定的排序算法。当输入的元素是 n 个 0 到 k 之间的整数时，时间复杂度是 O(n+k)，空间复杂度也是 O(n+k)，其排序速度快于任何比较排序算法。当 k 不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。