二叉树的定义
在计算机科学中,二叉树(Binary tree)是每个节点最多只有两个分支(即不存在分支度大于 2 的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒[1]。。
二叉树的性质
- 在二叉树的第 i 层上最多有 2^(i-1)个结点(i>=1)
- 深度为 h 的二叉树,最多有 2^h-1 个结点,最少有 h 个结点(h>=1)
- 包含 n 个结点的二叉树的高度至少为(log2n)+1
- 非空的二叉树,分支度为 0 的总数为 n0,分支度为 2 的总数为 n2,则 n0=n2+1
- 二叉树的总结点数 n = n1 + n2 + n0
- 总连线数等于总节点数减一(B = n - 1)
- 总连线数等于分支度为 2 的节点的两倍加上分支度为 1 的节点(B = n2 _ 2 + n1 _ 1)
二叉树的类型
满二叉树
一棵深度为 k 且有 2k-1 个节点的二叉树称为满二叉树。 除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树[2]。
完全二叉树
一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为 i(1≤i≤n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
二叉搜索树
二叉搜索树(BST)又称二叉查找树或二叉排序树。它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
平衡二叉树
平衡二叉树(AVL)一定是二叉搜索树,且左子树和右子树的高度差的绝对值不超过 1。 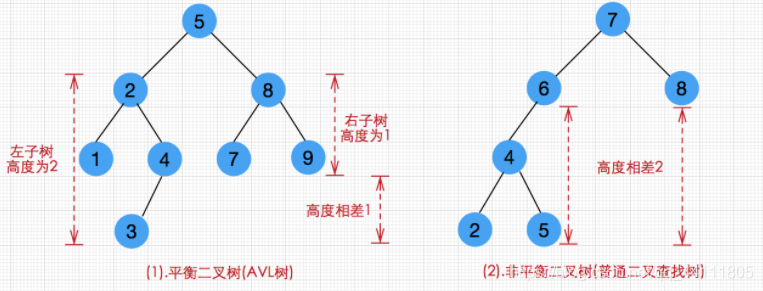
B 树
B 树属于多叉树又名平衡多路查找树(查找路径不只两个)
B+树
B+树是 B 树的变体,也是一种多路搜索树。
B*树
B* 树是 B+树的变体,在 B+树的非根和非叶子结点再增加指向兄弟的指针;B* 树定义了非叶子结点关键字个数至少为(2/3)M,即块的最低使用率为 2/3(代替 B+树的 1/2)。B 树分配新结点的概率比 B+树要低,空间使用率更高;
红黑树
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于 1,所以红黑树不是严格意义上的平衡二叉树(AVL),但对它进行平衡的代价较低, 其平均统计性能要强于 AVL 。
堆
遍历
前序遍历
后序遍历
中序遍历
层序遍历
常见算法题
镜像二叉树
重建二叉树
二叉树深度
二叉树节点总数
判断二叉树子结构
输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。(ps:约定空树不是任意一个树的子结构)